ICOSAEDRO (AQUI EL NOMBRE DE MI POLIEDRO)
A continuación se encontrará información sobre el poliedro XXX.
Este trabajo fue realizado por (aquí escribe su nombre).
Si quiere puede agregar correo electrónico de contacto.
.png)
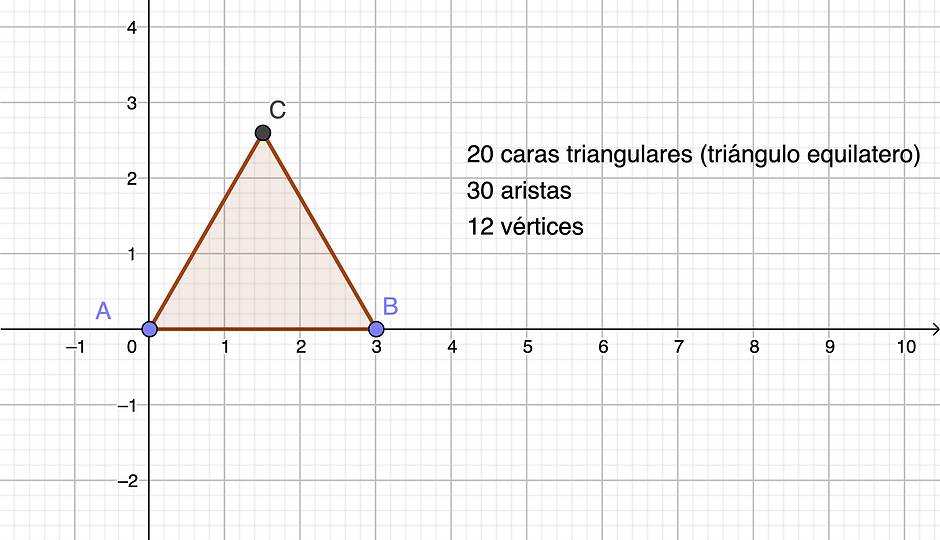
Entrega 1: composición del poliedro
Número de caras, ángulos planos, vértices y aristas.
La fórmula de Euler (o característica de Euler) en este caso se satisface:
V+C=2+A
12+ 20 = 30 + 2
Entrega 2: Geogebra y movimientos
En este enlace puede visualizar la construcción del poliedro en GeoGebra.
https://www.geogebra.org/classic/erbct2wz
Además se puede distinguir una rotación en ángulo de 72º.
.png)
Entrega 3: volumen del poliedro
Descomposición del poliedro en diversos poliedros
.png)
Entrega 4: ¿existe una esfera de modo que él poliedro este inscrito en ella?
En este caso sí existe una esfera.
Esto esta relacionado con el siguiente Teorema (libro Polyhedra, autor P.Cronwell teorema pág. 77):
Sea P un poliedro convexo cuyas caras son polígonos regulares congruentes.
Entonces las siguientes proposiciones son equivalentes:
1. Los vértices de P viven en la esfera.
2. Todos los ángulos diedros en P son iguales.
3. Todos los vértices, son vértices de polígonos regulares.
4. Todos los ángulos sólidos son congruentes
5. Todos los vértices son conformados por el mismo numero de caras.
_edited.jpg)
%2011_03_34.png)